5 room puzzle variants  | diagram with xvi openings/doors
 | 3D rendering of the puzzle
 | This erstwhile pop puzzle, called "Five Room Business firm puzzle" (as well known as "Walls and Lines puzzle", or "Cross the Network puzzle"), is canonically represented every bit a rectangular diagram divided into five rooms, as shown reverse. The object of the puzzle is to depict a continuous path through the walls of all 5 rooms, without going through whatever wall twice, and without crossing whatsoever path. The path can, of grade, end in any room, non necessarily in the room from where information technology started. Some puzzle diagrams represent the rooms with openings supposed to be doors. In this instance, the challenge is to visit every room of the apartment by walking through every door exactly once. Requirements for solvability
Whether starting and ending in the same room, or starting in i room and catastrophe in some other i, every other room of the diagram/apartment must have an even number of doors... That is, pair(s) of 'in' and 'out' doors (equally doors CANNOT be used TWICE, nosotros have then to use an even number of doors every bit we ENTER and Go out those rooms). Permit'southward suppose we start in a room with an odd number of doors, then it is possible to visit all the v rooms of the apartment if and But if some other room has an odd number of doors - representing the departure and the arrival points of the continuous path - , and all the other rooms accept an even number of doors. In a few words, for this topological puzzle to be solvable, at that place may NOT be more than than TWO rooms with an odd number of doors. Since the puzzle has THREE rooms with an odd number of openings/doors, it is mathematically impossible to complete a excursion crossing. Analogously, a continuous line that enters and leaves one of the rooms crosses 2 walls. Since the Iii contiguous larger rooms each have an odd number of walls to exist crossed, it follows that an Terminate of a line must be inside each of them if all the 16 walls are crossed. But a unicursal line has merely TWO ends, this contradiction makes the 5 Room House puzzle unsolvable. However, if nosotros close a door or add an extra room to the puzzle (meet fig. a and b below), then it becomes solvable. Now, yous tin can easily depict one continuous line that passes through every opening exactly once... Endeavour it! (the v-room variant on the left (fig. a) is just a little harder to solve, because yous have to figure out where to start) 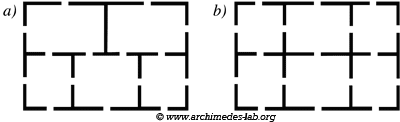 The Five Room House is actually a classic example of an incommunicable puzzle — one that bears no positive solution. In this particular case, the solution consists in finding that the problem has no solution! (remember: puzzles always take one, several or no solutions; see tips to puzzle solving) Graph theory
 The insolubility of the 5 Room House trouble can be proved using a graph theory approach, with each room being a vertex and each wall existence an edge of the graph (run across paradigm opposite). In fact, this puzzle is similar to the famous "7 bridges of Königsberg" problem thanks to which the eminent Swiss mathematician Leonhard Euler laid the foundations of graph theory.
Euler wondered whether there was a mode of traversing each of the 7 bridges over the river Pregel at Königsberg (at present Kaliningrad) once and merely one time, starting and returning at the same point in the town. He finally realized that the problem had no solutions! |
|   Tricks to 'solve' the puzzle
As yous experienced, this puzzle is impossible to solve on paper... Just 'incommunicable' puzzles sometimes take out-of-the-box solutions, as the not-standard solution depicted beneath. 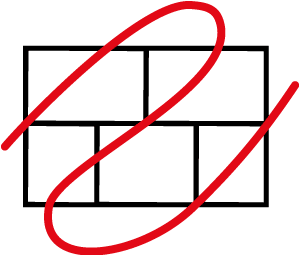 Some other neat out-of-the box solution...
Everything down to this bespeak has been in 2 dimensions, either a diagram fatigued on paper, or a five room apartment on a flat surface. In order to describe a continuous path that goes from one room to some other without crossing a line or going through a door twice, you have to reproduce the five room house puzzle onto a surface that is not topologically equivalent to a canvass of paper. The solid that may help yous is a torus, a kind of ring-shaped solid resembling a doughnut or a bagel. The puzzle diagram should be reproduced so that the hole of the torus is inside ane of the 3 larger rooms, equally shown in the instance below.   All the Well-nigh Wanted Puzzle Solutions in a look!  |
"Tin can anyone solve the following puzzle? Information technology's elementary as hell, but I can't figure it out... The thought is, you are supposed to draw this grid on a piece of paper, then depict one continuous line, starting anywhere, which crosses every grid bar once. I spent a long time on this trouble, but all the same take no solution, please aid me!" -- Robert
